Las nociones de sistemas formales nos dan herramientas para hablar de lo que se puede demostrar dentro de un sistema de axiomas dado. Un sistema así se llama completo si, para cada fórmula bien formada f, se puede demostrar f o ¬f usando sólo las reglas de inferencia. Es posible a priori o al menos pensable que existen sistemas donde hay fórmulas bien formadas f de las cuales ni f ni tampoco ¬f se pueden derivar usando nada más que las reglas de inferencia. En este caso f es independiente de los axiomas dados y es posible aumentar el conjunto de axiomas por f o por ¬f .
Hay varios casos conocidos de axiomas que son independientes de otros como, por ejemplo, el quinto postulado de Euclides mencionado anteriormente, que es independiente de los otros cuatro postulados. Si se sustituye por su negación, se obtienen las geometrías noeuclidianas. También la hipótesis del continuo es independiente de los axiomas ZFC; esta hipótesis afirma que cada subconjunto de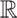 
, el conjunto de los números reales, tiene la misma cardinalidad 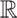que o que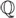 
, pero no hay nada intermedio.
Lo que pedía Hilbert en su programa era dar un conjunto de axiomas que establecieran las bases para todas las matemáticas, como se hacía en el libro Principia Mathematica para la aritmética y, luego, demostrar que este sistema de axiomas era completo. Pero eso no es posible, según lo comprobó Kurt Gödel, un matemático que nació en 1906 en Austria y murió en 1978 en Estados Unidos.
El resultado que demostró se llama hoy el teorema de Gödel y afirma que un sistema axiomático consistente y "suficientemente poderoso para describir los números enteros" es necesariamente incompleto. Consecuentemente, en cualquier sistema formal que incluya la aritmética como se hace en Principia Mathematica, siempre habrá fórmulas bien definidas que no se puedan derivar ni tampoco su contrario. En otras palabras, siempre habrá afirmaciones en las que no podremos decidir si son verdaderas o falsas.
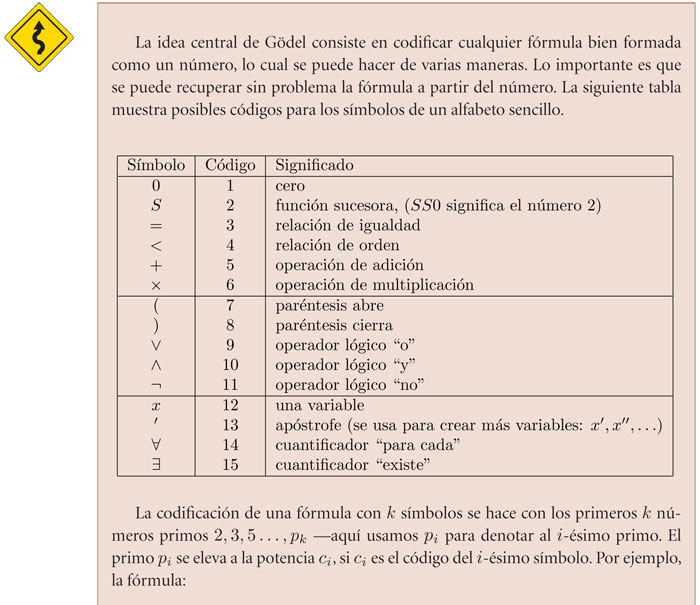
Así es como Gödel llega a la conclusión de que cualquier sistema que sea lo suficientemente poderoso para poder operar con números naturales, siempre contendrá afirmaciones que no son demostrables ni tampoco su negación.
Con ello, concluimos este viaje por la lógica. En resumen, cualquier formalización que incluye la aritmética es necesariamente incompleta. Por lo tanto, cualquier formalización de todas las matemáticas, necesariamente, es incompleta. En este sentido, los puntos 2 y 3 del programa de Hilbert no son compatibles: si el sistema es consistente, es necesariamente incompleto.
Lo anterior puede parecer desalentador, ya que con ello se derrrumbó el ambicioso programa de Hilbert. Por otro lado, se puede ver como una invitación para hacer matemáticas, ya que éstas no se pueden realizar completamente dentro de sistemas formales. La demostración misma del Teorema de Gödel es una joya de razonamiento que no se da en un sistema formal, sino que se razona sobre ellos. Visto de esta manera, podríamos interpretar este resultado como una confirmación de la importancia para la creatividad del intelecto humano dentro de las matemáticas.
